For the upcoming math test, I'll have the instant-kill trigonometry. So here I recap you with trigonometry integrals and other formulas which I think will be useful for solving problems. Original site here.
Basic definition of trigonometric function:
That's pretty much for the upcoming exam. Hope can do it at that time -_-".
Pray for me folks!
Basic definition of trigonometric function:
- A.)
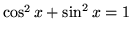
- B.)
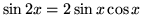
- C.)
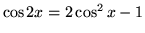 so that
so that 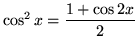
- D.)
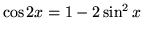 so that
so that 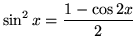
- E.)
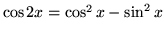
- F.)
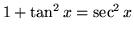 so that
so that 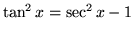
- G.)
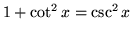 so that
so that 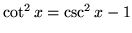
- 1.)
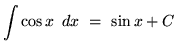
- 2.)
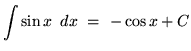
- 3.)
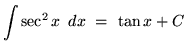
- 4.)
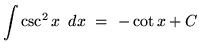
- 5.)
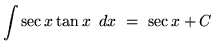
- 6.)
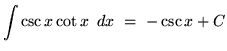
That's pretty much for the upcoming exam. Hope can do it at that time -_-".
Pray for me folks!
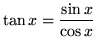
yAY!!! Matnya gampang!!! XD XD
BalasHapusHooh, payah ni wa nulis banyak2x -_-"
BalasHapus